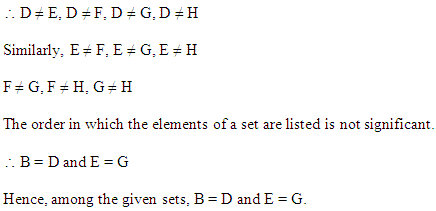NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.2

NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.2

Get Free NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.2 PDF in Hindi and English Medium. Sets Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Sets Exercise 1.2 Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 1 Class 11 Sets Ex 1.2 provided in NCERT Textbook.

Class 11 Maths NCERT Solutions Chapter 1 Sets Ex 1.2

Q.1: Which of the following given below is null set?
(i).  Set of odd natural numbers which is divisible by 2.
(ii).  Set of even numbers which are prime
(iii).  {x: x is a natural number, x<5 and x>7}
(iv).  {y: y is a point common to any two parallel lines}

Solution:

Q.2:  State whether the following sets are infinite or finite:
(i).  A set of months of a year.
(ii).  {1, 2, 3 ….}
(iii).  {1, 2, 3…99, 100}
(iv).  The set of positive integers which are greater than 100.
(v).  The set of prime numbers which are less than 99

Solution: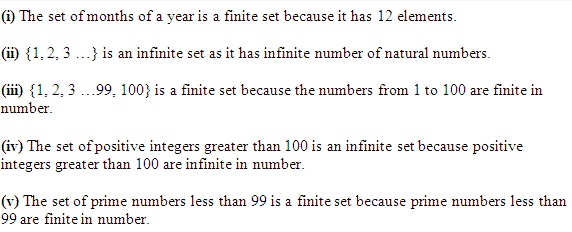

Q.3: State whether the following sets are infinite or finite:
(i).  The set of lines parallel to the x – axis.
(ii).  The set of letters in the vowels.
(iii).  The set of numbers multiple of 10.
(iv).  The set of humans living on Earth.
(v).  The set of circles passing through the origin (0, 0).

Solution:

Q.4: In the following set given below, state whether A = B or not:
(i).  A = {w, x, y, z}
B = {z, y, x, w}
(ii).  A = {5, 9, 13, 17}
B = {9, 5, 17, 19}
(iii).  A = {4, 2, 6, 10, 8}
B = {x: x is positive even integer and x≤10 }
(iv).   A = {x: x is a multiple of 10}
B = {10, 15, 20, 25, 30 …}

Solution:

Q.5 In the following set given below, is the pair of sets equal?
(i). A = {3, 4}
B = {y: y is solution of y²+5y+6=0}
(ii).  A = {a: a is a letter in the word FOLLOW}
B = {b: b is a letter in the word WOLF}

Solution:

Q.6: From the following sets, select equal sets:
A = {2, 4, 8, 12}
B = {1, 2, 3, 4}
C = {4, 8, 12, 14}
D = {3, 1, 4, 2}
E = {–1, 1}
F = {0, a}
G = {1, –1}
H = {0, 1}

Solution: