NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.4
NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.4
Get Free NCERT Solutions for Class 11 Maths Chapter 1 Sets Ex 1.4 PDF in Hindi and English Medium. Sets Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Sets Exercise 1.4 Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 1 Class 11 Sets Ex 1.4 provided in NCERT Textbook.
Class 11 Maths NCERT Solutions Chapter 1 Sets Ex 1.4
Q.1: Find the union of each of the following pairs of sets:
(i). P = {1, 4, 6} and Q = {1, 3, 4}
(ii). X = {a, e, i, o, u} and Y = {x, y, z}
(iii). X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 6}
(iv). X = {x: x is a natural number and 1 < x ≤ 5} and Y = {x: x is a natural number and 5 < x < 10}
(v). X = {4, 5, 6} and Y = Φ
Solution:
Q.2: Let A = {x, y} and B = {x, y, z}
Is A ⊂ B? What is A ∪ B?
Solution: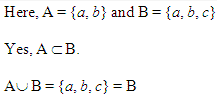
Q.3: If X and Y are two sets such that X ⊂ Y, then what is X ∪ Y?
Solution:![]()
Q.4: If P = {1, 2, 3, 4}, Q = {3, 4, 5, 6}, R = {5, 6, 7, 8} and S = {7, 8, 9, 10}
Find the following:
(i). P ∪ Q
(ii). P ∪ R
(iii). Q ∪ R
(iv). Q ∪ S
(v). P ∪ Q ∪ R
(vi). P ∪ Q ∪ S
(vii). Q ∪ R ∪ S
Solution: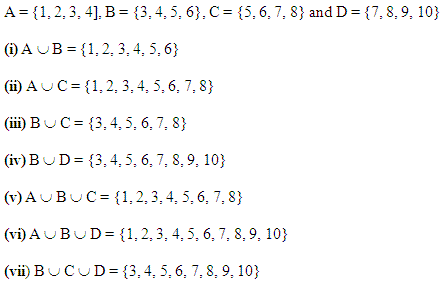
Q.5: Find the intersection of each of the following pairs of sets:
(i). P = {1, 4, 6} and Q = {1, 3, 4}
(ii). X = {a, e, i, o, u} and Y = {x, y, z}
(iii). X = {x: x is a natural number and multiple of 3} and Y = {x: x is a natural number less than 6}
(iv). X = {x: x is a natural number and 1 < x ≤ 5} and Y = {x: x is a natural number and 5 < x < 10}
(v). X = {4, 5, 6} and Y = Φ
Solution 5: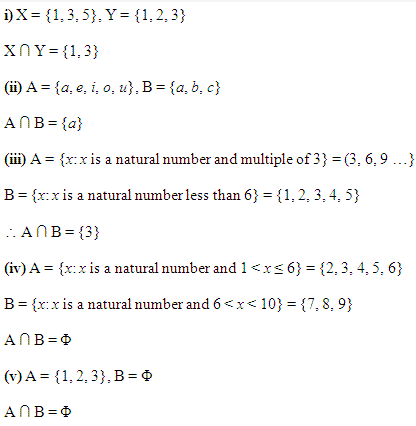
Q.6: If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15} and D = {15, 17}
Find the following:
(i). A ∩ B
(ii). B ∩ C
(iii). A ∩ C ∩ D
(iv). A ∩ C
(v). B ∩ D
(vi). A ∩ (B ∪ C)
(vii). A ∩ D
(viii). A ∩ (B ∪ D)
(ix). (A ∩ B) ∩ (B ∪ C)
(x). (A∪ D) ∩ (B ∪ C)
Solution:
Q.7: If A = {y: y is a natural number}, B ={y: y is an even natural number}, C = {y: y is an odd natural number} and D = {y: y is a prime number}
Find the following:
(i). A ∩ B
(ii). A ∩ C
(iii). A ∩ D
(iv). B ∩ C
(v). B ∩ D
(vi). C ∩ D
Solution 7:
Q.8: Which of the given pairs of sets are disjoint?
(i). A = {1, 2, 3, 4} and B = {x: x is a natural number and 4 ≤ x ≤ 6}
(ii). A = {a, e, i, o, u} and B = {c, d, e, f}
(iii). A = {x: x is an even integer} and B = {x: x is an odd integer}
Solution: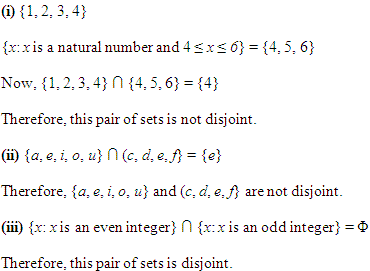
Q.9: If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16} and D = {5, 10, 15, 20}
Find the following:
(i). A – B
(ii). A – C
(iii). A – D
(iv). B – A
(v). C – A
(vi). D – A
(vii). B – C
(viii). B – D
(ix). C – B
(x). D – B
(xi). C – D
(xii). D – C
Solution 9: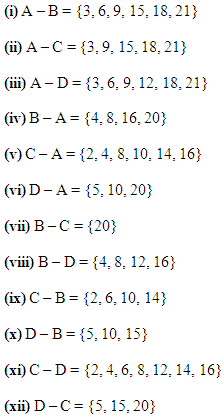
Q.10: If X = {a, b, c, d} and Y = {f, b, d, g}
Find the following:
(i). X – Y
(ii). Y – X
(iii). X ∩ Y
Solution: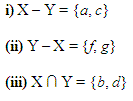
Q.11: What is R – Q, if R is the set of real numbers and Q is the set of rational?
Solution: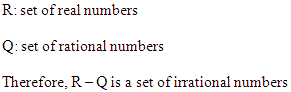
Q.12: State whether the following statements are true or false. Give reason.
(i). A = {2, 3, 4, 5} and B = {3, 6} are disjoint sets.
(ii). A = {a, e, i, o, u } and B = {a, b, c, d} are disjoint sets.
(iii). A = {2, 6, 10, 14} and B = {3, 7, 11, 15} are disjoint sets.
(iv). A = {2, 6, 10} and B = {3, 7, 11} are disjoint sets.
Solution:





